Next: Error analysis
Up: Derivation of solution
Previous: Derivation of solution
It should be mentioned that for the sake of
numerical stability, the measured points 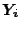 should be
translated if necessary into a coordinate system whose origin is close
to the mean of the points. This stability can be achieved
automatically, and the computation simplified somewhat, by
reformulating the solution in the following way.
should be
translated if necessary into a coordinate system whose origin is close
to the mean of the points. This stability can be achieved
automatically, and the computation simplified somewhat, by
reformulating the solution in the following way.
First, solve for 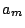 from the last of the equations
(13):
from the last of the equations
(13):
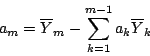 |
(14) |
where
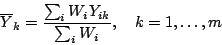 |
(15) |
This shows that the point
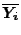 lies on the best-fit
hyperplane. Now define
lies on the best-fit
hyperplane. Now define
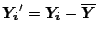 and
and
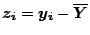 .
From Equations (8) and (9) we have
.
From Equations (8) and (9) we have
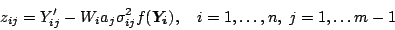 |
(16) |
where we can express 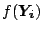 as
as
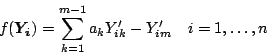 |
(17) |
Then upon
inserting (14) into the remaining equations
(13) we find
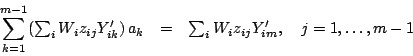 |
(18) |
This reformulation has improved the numerical stability and reduced the
order of the set of equations that needs to be solved on each
iteration by 1.



Next: Error analysis
Up: Derivation of solution
Previous: Derivation of solution
Robert Moniot
2002-10-20
![]() from the last of the equations
(13):
from the last of the equations
(13):