


Next: Bibliography
Up: Least-Squares Fitting of a
Previous: Refinement
The variances of the hyperplane parameters
can be found by evaluating
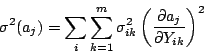 |
(19) |
(This equation assumes the data 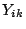 are uncorrelated.) Since the
dependence of
are uncorrelated.) Since the
dependence of  on
on 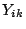 is not linear as
Equation (13) suggests, due to the dependence of
is not linear as
Equation (13) suggests, due to the dependence of
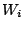 and
and 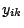 on
on  , evaluation of this expression is very
complicated. The original version of this paper contained an error in
the result of this calculation, and a corrected calculation has not
yet been done. To first order, however, ignoring the nonlinearity one
obtains the approximation
, evaluation of this expression is very
complicated. The original version of this paper contained an error in
the result of this calculation, and a corrected calculation has not
yet been done. To first order, however, ignoring the nonlinearity one
obtains the approximation
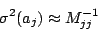 |
(20) |
that is, the variances of the parameters are given simply by the
diagonal elements of the inverse of the normal matrix defined in
Equation (13). (The
off-diagonal elements of this matrix are the covariances of the
parameters.) For well-behaved data such as those used for
illustration by York (1966), this approximation is good to within a
few percent.
If the experimenter does not have standard errors 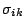 for
the measured quantities
for
the measured quantities 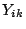 , but only relative uncertainties, the
resulting fit is the same using these relative uncertainties, but the
variances in the fitted parameters are given by
expression (20) multiplied by
, but only relative uncertainties, the
resulting fit is the same using these relative uncertainties, but the
variances in the fitted parameters are given by
expression (20) multiplied by 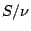 ,
where
,
where 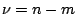 is the number of degrees of freedom of the
problem. If the errors
is the number of degrees of freedom of the
problem. If the errors 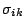 are known a priori, then the
goodness of fit can be inferred from the value of
are known a priori, then the
goodness of fit can be inferred from the value of 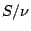 , which
should be close to unity for normally distributed errors. This
constitutes a test of the
, which
should be close to unity for normally distributed errors. This
constitutes a test of the 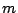 -component hypothesis as set forth in
the introduction.
-component hypothesis as set forth in
the introduction.



Next: Bibliography
Up: Least-Squares Fitting of a
Previous: Refinement
Robert Moniot
2002-10-20
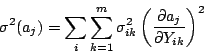
![]() for
the measured quantities
for
the measured quantities ![]() , but only relative uncertainties, the
resulting fit is the same using these relative uncertainties, but the
variances in the fitted parameters are given by
expression (20) multiplied by
, but only relative uncertainties, the
resulting fit is the same using these relative uncertainties, but the
variances in the fitted parameters are given by
expression (20) multiplied by ![]() ,
where
,
where ![]() is the number of degrees of freedom of the
problem. If the errors
is the number of degrees of freedom of the
problem. If the errors ![]() are known a priori, then the
goodness of fit can be inferred from the value of
are known a priori, then the
goodness of fit can be inferred from the value of ![]() , which
should be close to unity for normally distributed errors. This
constitutes a test of the
, which
should be close to unity for normally distributed errors. This
constitutes a test of the ![]() -component hypothesis as set forth in
the introduction.
-component hypothesis as set forth in
the introduction.